MySQL 索引结构
MySQL 索引结构
1.常见的数据结构
众多的数据结构在逻辑层面可分为线性结构和非线性结构。
- 线性结构:数组、链表、哈希表、队列、栈等
- 非线性结构:树、图、跳表、位图等
2.选哪种数据结构作为索引结构
2.1 选择作为索引的要求
- 要尽少在磁盘上做I/O操作。
- 要能尽快的按照区间高效地范围查找
2.2 哈希表
哈希表是我们再熟悉不过的,数据以key-value的形式存储,哈希表拥有精确的查询(时间复杂度为O(1))。
哈希表之所以能这么快是通过key能迅速找到对应的value,最简单的方式是余数法,通过计算key的HashCode,再通过哈希表的长度对HashCode求余,求余得出的余数就是数组下标,最后由下标访问到哈希表中存的Key、Value。
但是key可能会冲突,这时候就需要用链表的方式解决,当发生冲突时,key相同形成一个链表,然后遍历整个链表就可以了。
虽然哈希表可以高效的等值查询,但是哈希表不支持区间查询,当用哈希表作为索引的结构时,进行范围查询时就要做全部扫描。
所以哈希表作为索引的数据结构不适合范围查询的场景。
2.3 跳表
跳表是redis比较常用的数据结构之一,跳表的本质就是可以进行二分查找的有序链表。在链表基础上加上索引层,既支持插入和删除等动态操作,也支持按区间高效查询,不管是查找、插入、删除对应的时间复杂度都是O(logN)。
要理解跳表,先看链表,假设链表要查询某一个数据,在最差的情况下要从头遍历整个链表时间复杂度为O(n)。
如下图,我们在链表的基础上加了索引层,可以起到区间查询的作用。

从上图所示,我们要查询一个26的节点,跳表就可以先从索引层遍历,当遍历在索引层21节点,会发现下一个索引层的节点是36节点,则明白要在【21-36】区间内查询26的节点。速度明显比链表快很多。
然而,当数据量特别大的时候,可能会有多级索引,相应的就会增加IO的次数,从而影响性能。
2.4 二叉搜索树
二叉树作为底层数据结构时,虽然时间复杂度为O(logN),但是二叉树也有明显的弊端。在极端情况下,如果每次插入的数据都是最小或者最大的元素,那么树结构会退化成一个链表,查询数据的时间复杂度就会是O(n)。这时你会想到自平衡二叉树,即让树中每个节点的左右子树高度差不能超过1。那么这样就可以让左右子树都保持平衡,让查询数据操作的时间复杂度在O(logn)。
虽然是自平衡树,但随着插入的元素增多,导致树的高度变高,同样意味着磁盘I/O操作次数多,影响整体查询的效率。
2.5 B 树
自平衡二叉树虽然查找的时间复杂度在O(logn),但它毕竟是个二叉树,每个节点只能有两个子节点,那么随着数据量增大的时候,节点个数变多,树的高度越来越高,磁盘IO读取次数就越来越大,影响查询效率。这时你会想到B树。
B树解决了二叉树每个节点只能有两个子节点的问题,而是允许M个子节点。不仅如此,B树的一个节点可以存储多个元素,相比较于二叉树,树的高度降低了。
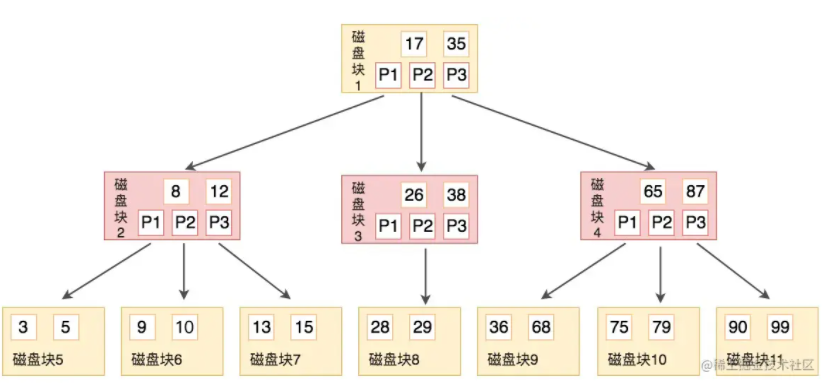
虽然B树满足了减少磁盘I/O操作,同时支持按区间查找的需求,但是B树在区间查找的问题上并不高效。例如,查询3-10之间的所有结点,因为B树做范围查询时使用的是中序查询,那么父节点和子节点也需要来回切换涉及了多个节点会给磁盘I/O带来很多负担。
2.6 B+树
B+树从名字就可以看出是B树的升级版,MySQL中innoDB引擎的索引底层数据结构就是使用的B+树。
B树相对于B树,做了这样的升级:B+树的非叶子节点都不存储数据,而是作为索引。由叶子节点存放整个树的所有数据。而叶子节点之间构成了一个从小到大的链表相互指向相邻的叶子节点,也就是叶子节点之间形成了有序的双向链表,如下图:

B树相比于B+树,B树没有冗余节点,删除节点时会发生复杂的树变形,而B+树有冗余节点,不会涉及到复杂的树变形。而且B+树的插入也是如此,最多只涉及树的一条分支路径。B+树也不用更多复杂算法,可以类似黑红树的旋转去自动平衡。